Briggs (1973) proposed a series of empirical formulae for the
determination of
![]() and
and
![]() :
:
| ||||||||||||||||||||||||||||||||||||||||||
- terrain effects on impingement and steering the plume
- vertical variations in stability
- horizontal or vertical variations in the wind field
- local circulations
- Puff models - treat emissions as a series of 'puffs' which are individually transported and dispersed (variant of GPM)
- Box models - based upon conservation of pollutant mass within a volume (often used in chemical transformation models, e.g. photochemical models)
- Gradient transport models - based upon flux/gradient (K) turbulent transport (GPM is a special case of this in which the eddy diffussivities are constant)
- Trajectory models - move a vertical column at the mean wind speed with pollutants added at the bottom as they are generated
- Mesoscale models / Lagrangian Particle Dispersion Models - mesoscale atmospheric models produce gridded mean wind fields, many particles are inserted into the wind field and are transported by the mean wind and diffused by a random element representing turbulence
 exp
exp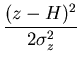
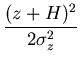
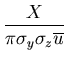 exp
exp